NOTIFICATION: These examples are provided for educational purposes. The use of this code and/or information is under your own responsibility and risk. The information and/or code is given ‘as is’. I do not take responsibilities of how they are used. You are welcome to point out any mistakes in my posting and/or leave a comment.
Some of the mathematical tools (known as number theory) use in network security are prime numbers, greatest common divisor (GCD), Fermat’s theorem, Euler Totient function and theorem, primality testing and Miller Rabin algorithm.
Prime Number
A prime number is an integer p greater than 1 which can only be divided by 1 and itself.
Formally speaking:
“A prime number (or prime integer, often simply called a “prime” for short) is a positive integer ![]() that has no positive integer divisors other than 1 and
that has no positive integer divisors other than 1 and ![]() itself. ” <http://mathworld.wolfram.com/PrimeNumber.html>
itself. ” <http://mathworld.wolfram.com/PrimeNumber.html>
An example of prime numbers: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, …
An example of numbers that are not prime: 1, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, …
In the website Math.com you can find a prime number calculator that can tell you if a number is prime or not: <http://www.math.com/students/calculators/source/prime-number.htm>
One of the ways we can use prime numbers is to factorize a number in a unique way:
Any number a greater than 1 can be factored in a unique way using prime p numbers while each consecutive prime number is greater than the previous prime number and their consecutive exponents b are one greater that then previous:
a = p1^b1 * p2^b2 * ... * pn^bn while p1 < p2 < ... < pn and (b1, b2, ..., bn) > 0
For example:
-
a = 91 = p1 ^ b1 * p2 ^ b2 = 7 ^ 1 * 13 ^ 1 = 7 * 13 Therefore, P1 = 7 and P2 = 13
-
a = 3600 = p1 ^ b1 * p2 ^ b2 * p3 ^ b3 = 2^4 * 3^2 * 5^2 Therefore, P1 = 2, P2 = 3, and P3 = 5
Greatest Common Divisor (GCD)
The greatest common divisor (gcd) is a number in which you can divide two positive numbers a and b and at the same time is common in a and b.
Formally Speaking:
“The greatest common divisor … of two positive integers ![]() and
and ![]() is the largest divisor common to
is the largest divisor common to ![]() and
and ![]() . ” <http://mathworld.wolfram.com/GreatestCommonDivisor.html>
. ” <http://mathworld.wolfram.com/GreatestCommonDivisor.html>
There are different ways to obtain the greatest common divisor such as using prime factorizations, Euclid’s algorithm, and others <http://en.wikipedia.org/wiki/Greatest_common_divisor>.
Approach 1:
A way to determine the greatest common divisor of two integers a and b is by
comparing the prime factorization of a and b and using their least powers.
Lets assume we wish to obtain the greatest common divisor of 12 and 30, gcd(12, 30).
For 300, we obtain the following prime numbers:
30 = 2^1 * 3^1 * 5^1
For 12, we obtain the following prime numbers:
12 = 2^1 * 3^1 = 2^1 * 3^1 * 5^0
In both cases, we have that 2 and 3 are the prime numbers used in a and b.
Also, we have that 2^1 and 3^1 are their least powers. Therefore,
gcd(12, 30) = 2^1 * 3^1 = 6
Approach 2:
The follow is a more friendly approach to obtain the greates common divisor.
Lets assume we wish to know the greatest common denominator of 7 and 160, gcd(7, 160)
- Write down this formula:
(Dividend) = (Divisor) * (Quotient) + (Remainder) - The greatest number will be the dividend:
Dividend = 160
(160) = (Divisor) * (Quotient) + (Remainder) - The other number will be the divisor:
Divisor = 7
(160) = (7) * (Quotient) + (Remainder) - Multiply the divisor with a quotient that would get you a number as close as possible to the dividend
If 160/7 = 22.8571429 then use 22 for the quotient
(160) = (7) * (22) + (Remainder) - The remainder will be the number that you need to reach 160. Since 7 * 22 is 154 the remainder is 6
(160) = (7) * (22) + (6) - Now the Divisor became the new dividend and the remainder became the new divisor:
New dividend = 7 (previous divisor)
New divisor = 6 (previous remainder)
(7) = (6) * (Quotient) + (Remainder) - Repeat the process, get a quotient that would multiply the divisor (6) as close as possible to the dividend (7)
(7) = (6) * (1) + (Remainder) - The remainder would be 1. This remainder is the greatest common divisor between 7 and 160
gcd(7, 160) = 1
You can find a gcd calculator here:
<http://britton.disted.camosun.bc.ca/gcdlcm/jbgcdlcm.htm>
Fermat’s Theorem
Before going over the Fermat’s theorem, let review an old concept related with this topic, modular arithmetic.
Modular arithmetic (also known as clock arithmetic), is a system in which numbers “wrap around” after reaching a certain value. Of this system, we use the congruence relation on integer known as modulus.
Formally speaking:
“For a positive integer n, two integers a and b are said to be congruent modulo n, (a = b mod n),
if their difference a − b is an integer multiple of n. The number n is called the modulus of the congruence” <http://en.wikipedia.org/wiki/Modular_arithmetic#Congruence_relation>
For Example:
-
Lets assume we have a = 100, b = 86, and n = 7 such that 100 = 86 (mod 7).
-
100 - 86 = 14 in which 14 has 7 as a divisor.
-
If we divide 100 by 7, we find out that the quwootient is 14 and remainder is 2.
-
Just coincidence, if we have 100 = 2 (mod 7), we also find out that the remainder (b) is two too.
Another way to see the previous example is as follows:
100 = 86 (mod 7) Means that 100 and 86 leave the same remainder when you divide by 7; or, equivalently, that their difference is a multiple of 7. Here is a link in which you can find the quotient and remainder of a division: <http://www.analyzemath.com/Calculators_3/quotient_remainder.html>
Another example:
-
For a = 0 mod 5, If a = 0 mod 5 then a^4 = 0^4 = 0 mod 5
-
For a = 1 mod 5, if a = 1 mod 5 then a^4 = 1^4 = 1 mod 5
-
For a = 2 mod 5, if a = 2 mod 5 then a^4 = 2^4 = 16 = 1 mod 5
-
For a = 3 mod 5, if a = 3 mod 5 then a^4 = 3^4 = 81 = 1 mod 5
-
For a = 4 mod 5, if a = 4 mod 5 then a^4 = 4^4 = 256 = 1 mod 5
Now that we have an idea about modulus, we can begin talking about Fermat’s Theorem.
Fermat’s theorem also known as “Fermat’s little theorem” (do not confuse with “Fermat’s last theorem”), establish that:
- If p is a prime number and for any integer a lower than the prime number p, a<p is a positive integer not divisible by the prime number p.

- Or, if p is a prime number then for any integer a, a^p – a will be evenly divisible by p.

- Or, if p is a prime and a is an integer relatively prime to p, then [a^(p−1)] − 1 will be evenly divisible by p.

(<http://en.wikipedia.org/wiki/Fermat’s_little_theorem>)
For example:
-
Lets assume p = 3 and a = 2Fermat's little theorem establish that
-

-
Then a^(p-1) = 2^(3 - 1) = 2^2 = 4
-
So, 1 = a^(p-1) mod p = 4 mod 3 = 1
In network security, Fermat’s little theorem is used in public key and primality testing.
Euler Totient Function ø(n)
The Euler Totient function is represented by ø(n) or φ(n) depending the author.
The Euler Totient function establish that:
- ø(n) is the number of possitive integers less than n and coprime (also known as relatively prime) to n
- Or the number of positive integers less or equal to n that are relatively prime to n, where 1 is counted as being coprime (relatively prime) to all numbers.
- Or, ø(n) returns the number of integers less than n (including 1) that are relatively prime to n.
Note: we say that two integers a and b are relatively prime if a and b have no common positive factor other than 1 or, if their greatest common divisor is 1. a is relatively prime to b if gcd(a, b) = 1.
A list of Euler’s Totient Function Values For n = 1 to 500, with divisor lists can be found in the following URL address: <http://primefan.tripod.com/Phi500.html>
For example:
- Lets n = 37 so ø(n) = ø(37) = 35. 37 can be divided by 1 and by 37.
Therefore, all integers from 1 to 36 are relatively prime to 37 - Lets n = 35 so ø(n) = ø(35) = 24. 35 can be divided by 1, 5, 7, and 35.
Therefore, integers 1, 2, 1, 2, 3, 4, 6, 8, 9, 11, 12, 13, 16, 17, 18, 19, 22, 23, 24, 26,
27, 29, 31, 32, 33, 34 are relatively prime to 35.
You may ask, I did you found these values (such as ø(35) = 24)?
To find these values:
- (Case 1) For n = p (a prime), we have that ø(p) = p – 1.
For Example: Lets p = 7 so ø (p) = ø(7), then ø (7) = 7 – 1 = 6.
Therefore ø(7) = 6 - (Case 2) When n = p^a (power of a prime).
The numbers with common factor with n are: p, 2p, 3p, . . . ,p^(a-1) * p
since there are p^(a-1) of them.
For example: Lets assume we have a prime number p = 5 and a is 2:
ø(p^a) = p^a – p^(a-1) = (p^(a-1)) * (p – 1) = (p^a) * (1 – 1/p)
ø(5^2) = 5^2 – 5^(2 -1) = (5^(2 – 1)) * (5 – 1) = (5^2) * (1 – 1/5)
ø(25) = 5^2 – 5 = 5 * (5 – 1) = (5^2) * (1 – 1/5) = 20
ø(25) = 20 and all integers relative prime to 25 are
1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 13, 14, 16, 17, 18, 19, 21, 22, 23, 24.
As a general case for the Euler’t Totient function ø(n), we have that:
- Let p be a prime integer dividing n integer so the integers divisible by p are:
p, 2p, 3p, 4p, . . . , (n/p)(p) where there are n/p number of integers. - Then, the number of integers not divisible by p are: n – n/p = n * (1 – 1/p)
- Let q be another prime number dividing n.
If we wish to find the number of integers divisible by neither p or q,
then deduct the n/q multiples of q such that q, 2q, 3q, . . . , (n/q)(q) - In case some elements of p and q are common, the n/pq multiples of pq are:
pq, 2pq, 3pq, . . . , (n/pq)(pq) so n/q – n/pq = (n/q)(1- 1/p) - Therefore the total of integers not divisible by p or q is:
n(1 – 1/p) – (n/q)(1 – 1/p) = n(1 – 1/p)(1 – 1/q)
General formula for Euler’s Totient Function ø(n):
ø(n) = n * (1 – 1/p1) * (1 – 1/p2) * . . . * (1 – 1/pm), where p1, p2, . . . , pm are prime factors of n and m is the total number of prime numbers.
Example:
Lets n = 60, p1 = 2, p2 = 4, p3 = 5 and ø(n) = n * (1 – 1/p1) * (1 – 1/p2) * (1 – 1/p3) then
ø( 60) = 60 * (1 – 1/2) * (1 – 1/3) * (1 – 1/5)
ø(60) = (60 – 60/2) * (1 – 1/3) * (1 – 1/5)
ø(60) = (60 – 30) * (1 – 1/3) * (1 – 1/5)
ø(60) = (30) * (1 – 1/3) * (1 – 1/5)
ø(60) = (30 – 30/3) * (1 – 1/5)
ø(60) = (30 – 10) * (1 – 1/5)
ø(60) = (20) * (1 – 1/5)
ø(60) = (20 – 20/5)
ø(60) = (20 – 4)
ø(60) = 16
All integers relative prime to 16 are:
1, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 49, 53, 59
Euler’s Totient Function ø(n) using two Prime Numbers:
Let have two prime number p and q such that p ≠ q so ø(pq) = ø(p)*ø(q) = (p-1)*(q-1) in which
- The set {1, 2, …, pq -1} of integers is less than pq
- The integers in the set {1, 2, …, pq – 1} are not relatively prime to pq:
{p, 2p, …, (q – 1)p} and {q, 2q, …, (p – 1)q} - ø(pq) = (pq – 1) – [(q-1) + (p-1)]
ø(pq) = pq – p – q +1
ø(pq) = (p-1) * (q-1)
ø(pq) = ø(p)*ø(q)
For example:
ø(n) = ø(pq) = (p-1) * (q-1)
ø(21) = ø(3 * 7)
ø(21) = (3 – 1) * (7 – 1)
ø(21) = 2 * 6
ø(21) = 12
(<http://home.earthlink.net/~usondermann/eulertot.html>)
Euler’s Theorem
Euler’s Theorem (also known as Fermat-Euler theorem) establish that for every positive integer a relatively prime to n then ![]()
For example:
- Lets a = 3 and n = 10 then
ø(n) = ø(pq) = (p-1) * (q-1)
ø(10) = ø(2*5) = (2 – 1) * (5 -1) = (1) * (4) = 4
a^ø(n) mod n = 1
3^ø(10) mod 10 = 1
3^4 mod 10 = 1
81 mod 10 = 1 - Lets a = 2 and n = 11 then
ø(n) = ø(p – 1)
ø(11) = ø(11 – 1) = 10
a^ø(n) mod n = 1
2^ø(11) mod 11 = 1
2^10 mod 11 = 1
1024 mod 11 = 1
Primality Testing
- Very large prime numbers selected at random are necessary for most of cryptographic algorithms.
- Naïve Algorithm: The objective of this algorithm is to divide a number a by all the numbers in turn that are less than the square root of a. This kind of algorithm works for small numbers, but it inefficient for large numbers.
Miller Rabin Algorithm
Miller Rabin algorithm (also known as Miller-Rabin Primality Test) is an algorithm that return a true or false value depending a given value n. Normally, If it outputs true, then n is “probably prime”, else then n is definitely composite.
Approach 1:
[Split Off Power of]: Lets n > 3 and n be odd, k > 0, and q odd so ![]()
- [Random Base] Choose a random integer a with 1 < a < n.
- [Odd Power] Set b = a^n (mod m) so if b = ±1 (mod n) then output true and terminate.
- [Even Powers] For any r with 1 <= r <= k – 1, if b^2^r = -1 (mod n) then output true and terminate else output false
(< http://modular.math.washington.edu/edu/2007/spring/ent/ent-html/node26.html>)
Approach 2:
- Lets n > 3 and n be odd, k > 0, and q odd so
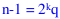 .
.
Divide (n – 1) by 2 until the result is an odd number. - Let a be an integer 1 < a < n where n > 2 so

Check which of the following two conditions is true:
(a) ( ) == true ?
) == true ?
(b) There exist 1 <= j <= k such that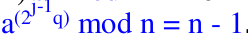 == true ?
== true ? - If any of the previous conditions (a and b) are true, then n may not be a prime number.
Example:
- Lets n = 2047 such that 2047 = 23 * 89.
- If
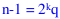 so n – 1 = 2^1 * 1023 then
so n – 1 = 2^1 * 1023 then - 2^1023 mod 2047 = 1
- However, 2047 is not a prime
Approach 3: (Similar to approach 1)
- Check if n integer value is prime or not
- If n is prime then find integers k > 0, q being odd, such that
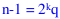 is true.
is true. - if
 is true then output is true (n maybe prime) else
is true then output is true (n maybe prime) else - Check for every value of j going from 1 to k if
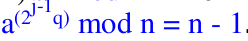 is true.
is true.
If true then output true (n maybe prime) else - return false (n is not prime)
Probabilistic Consideration
For an odd no prime number n and a randomly chosen integer a where 1 < a < n -1,
we can expect a probability of failure in detecting that n is not a prime number of less than one quarter of the probabiblities.
If we repeat the Millan Rabin algorithm with different values of a, there is a chance that we find a “maybe” prime number n after trying a t number of tests:
Probabilities of finding a “maybe” prime number n after t test are:
Pr(n maybe a prime number after t tests) = (1/4)^t
For example:
Lets assume we wish perform t = 10 tests using different values of a, we have less than 10^-6 probabilities to find an n that maybe a prime number.
Extra Examples
Lets have a = b mod p such that we wish to know a, b = 5^6 and p is 23 so a = 5^6 mod 23
How can we solve this? Using Modulus Arithmetic. One of the properties say that C^(ab) mod p = (C^a mod p)^b mod p
So,
5^6 mod 23 => 5^(2*3) mod 23 => (5^2 mod 23)^3 mod 23 => (25 mod 23)^3 mod 23
The remaider of 25 mod 23 is 2 (23 = 0, 24 = 1, 25 = 2) or you could divide 25 by 23: 23 * 1 = 23 => 25 – 23 = 2 remainer
(25 mod 23)^3 mod 23 => (2)^3 mod 23 => 8 mod 23 = 8 (is less than 23 so is inside the modulus)
© 2010, Alejandro G. Carlstein Ramos Mejia. All rights reserved.
