Facts
- The Ford-Fulkerson method
is iterative
- This method depends on three ideas:
- Augmenting paths
- Residual networks
- Cuts
- Simplified Pseudo-code:
initialize flow f to 0 while there exist an augmenting path p do augmented flow f along p return f
- An augmenting path
is a simple path from source
to sing
in the residual network
- Each path have alternative free and matched edges in such way that begins and ends with free vertices.
- Definition: Each edge
on an augmenting path admits some additional positive flow
to
without violating the capacity constrain on the edge.
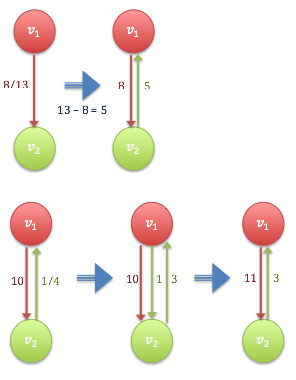
- Example:
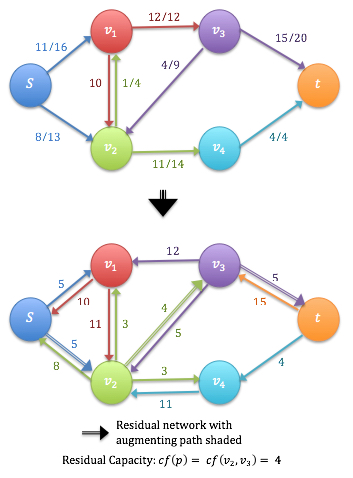
Cuts
- Minimum cut of a network: A cut whose capacity is minimum over all cuts on the network.
- Max-flow min-cut theorem: A flow is maximum if and only if its residual network contains no augmenting path.
- Example:
 Net-flow Across Cut (including net-flow between vertices):
Net-flow Across Cut (including net-flow between vertices):
Capacity (only edges going from sourceto sink
):
Pseudocode
// Comments
Ford-Fulkerson
for each edge
do //
:flow
do
while there exist a path from
to
in the residual network
do is in
//
: residual capacity
for each edge in
do //
: path
do
Big O
Using either dept-first search or breadth-first search, the time to find a path in a residual network is
Total running time is where
is the maximum flow found
Note: If you find any mistake please let me know
© 2015, Alejandro G. Carlstein Ramos Mejia. All rights reserved.
